算法高效进阶-A班 比赛总结

A. 骑上彩虹

1

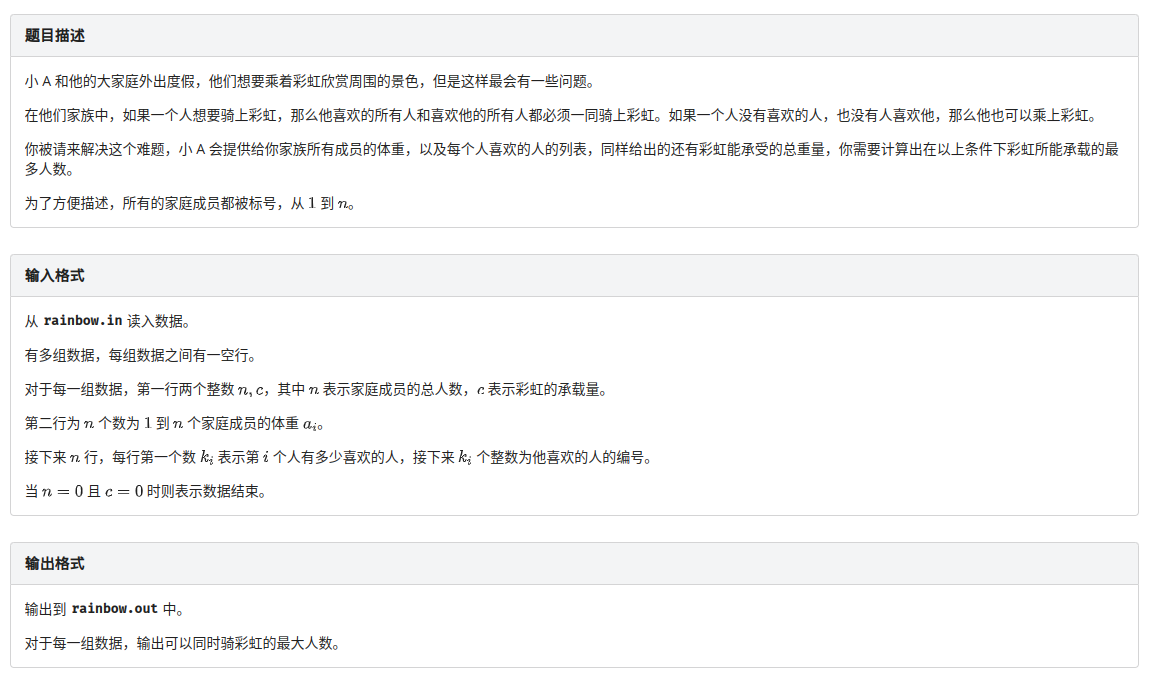
看到一个人想要骑上彩虹，那么他喜欢的所有人和喜欢他的所有人都必须一同骑上彩虹，考虑并查集，题目求彩虹能承载的最多人数，考虑01背包算法

首先将求并查集数组，路径压缩到根节点，新建数组$peo[MAXN]$，表示根节点人骑上彩虹时同时要骑上去的人数，子节点设为0，新建数组$aft[MAXN]$，表示根节点人上去需要的质量，从01背包的角度看，质量看成价值，人数看成占的容量就行了

代码如下：

#include <bits/stdc++.h>
namespace zxgaer = std;
using namespace zxgaer;
const int MAXN = 1005;
int bcj[MAXN];  //并查集数组
int aft[MAXN];  //加起来的质量数组
int a[MAXN];    //质量数组
int peo[MAXN];  //加起来的人数数组
int n, c;
int Find(int x) { return bcj[x] == x ? x : bcj[x] = Find(bcj[x]); }
void Merge(int x, int y) { bcj[Find(max(x, y))] = Find(min(x, y)); }
int main() {
    //freopen("rainbow.in", "r", stdin);
    //freopen("rainbow.out", "w", stdout);
    while (1) {
        scanf("%d%d", &n, &c);
        memset(aft, 0, sizeof(aft));
        memset(peo, 0, sizeof(peo));
        if (n == 0 && c == 0)
            return 0;
        for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
        for (int i = 1; i <= n; i++) bcj[i] = i;
        for (int i = 1; i <= n; i++) {  //这里处理并查集
            int p, q;
            scanf("%d", &p);
            for (int j = 1; j <= p; j++) {
                scanf("%d", &q);
                Merge(i, q);
            }
        }
        for (int i = 1; i <= n; i++) {  //这里处理总人数和总质量
            int fa = bcj[i];
            aft[fa] += a[i];
            peo[fa]++;
        }
        memset(bcj, 0, sizeof(bcj));  //这之后并查集数组没用，清空后当dp数组跑01背包
        for (int i = 1; i <= n; i++) {
            if (aft[i] != 0) {
                for (int j = c; j >= aft[i]; j--) bcj[j] = max(bcj[j], bcj[j - aft[i]] + peo[i]);
            }
        }
        int maxn = 0;
        for (int i = 0; i <= c; i++) maxn = max(maxn, bcj[i]);
        cout << maxn << endl;
    }
}

B. 最小方差

2

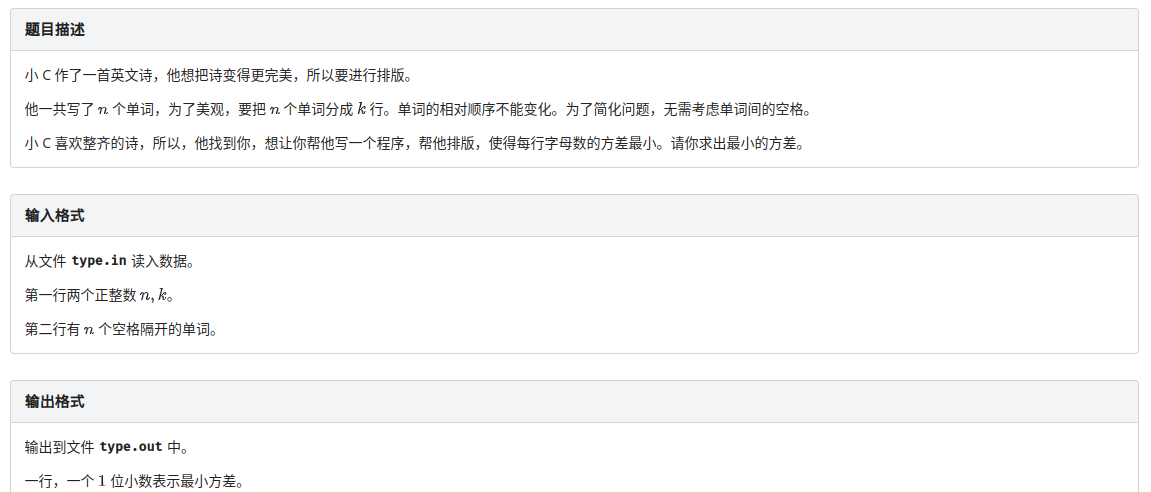
此题应该是洛谷P2112 鸿雁传书的改编版

题目中说不能把单词拆开，那么把每个单词看成一个数，这个数就是这个单词的字符数，换行就是分段，于是原题就可看成是数列分段

#include <bits/stdc++.h>
#define rep(i, a, b) for (int i = a; i <= b; i++)

namespace zxgaer = std;
using namespace zxgaer;
const int MAXN = 1005;
int n, k;
double a[MAXN], dp[MAXN][105];
double s[MAXN];
double ave;
string str;
int main() {
    //freopen("type.in", "r", stdin);
    //freopen("type.out", "w", stdout);
    scanf("%d%d", &n, &k);
    rep(i, 1, n) {
        cin >> str;
        a[i] = str.size();
        ave += a[i];
        s[i] = s[i - 1] + a[i];
    }
    ave /= k;
    rep(i, 1, n) rep(j, 2, k) dp[i][j] = 0x7fffffff;
    rep(i, 1, n) dp[i][1] = (s[i] - ave) * (s[i] - ave) / k;
    rep(j, 2, k) rep(i, j, n) rep(l, 1, i - 1) dp[i][j] =
        min(dp[i][j], dp[l][j - 1] + (s[i] - s[l] - ave) * (s[i] - s[l] - ave) / k);
    printf("%.1lf", dp[n][k]);
    return 0;
}

C. 逆序对数

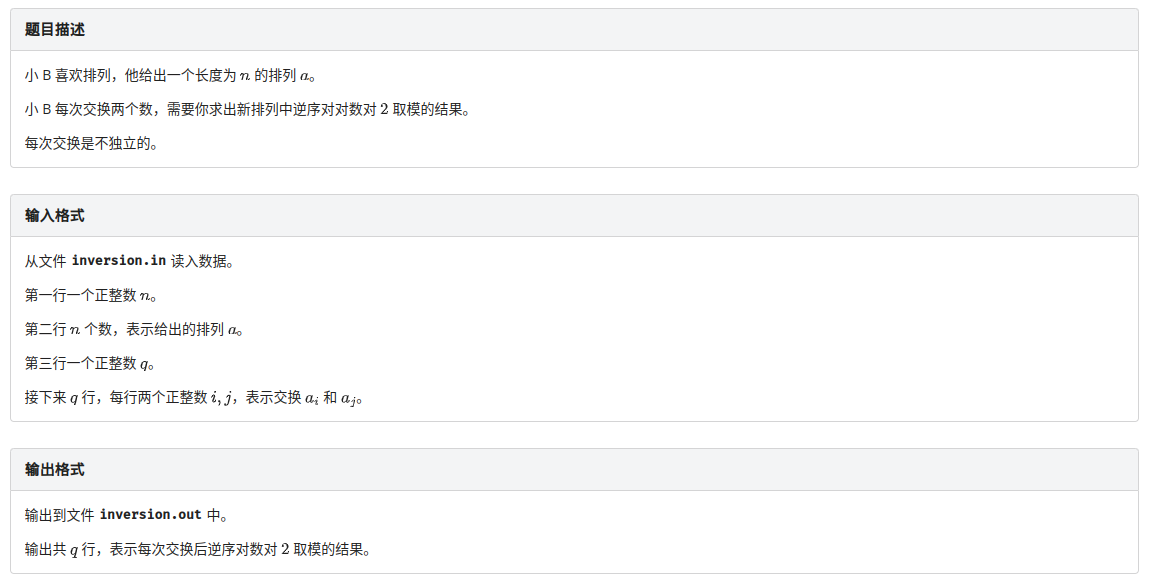
逆序对问题的经典做法就是树状数组和线段树，这里使用树状数组

#include <bits/stdc++.h>
#define rep(i, a, b) for (int i = a; i <= b; i++)

#define urep(i, a, b) for (int i = a; i >= b; i--)

#define lowbit(x) (x & -x)

namespace zxgaer = std;
using namespace zxgaer;
const int MAXN = 100005;
int n, q, nums[MAXN], f[MAXN], temp;
void add(int x, int y) {
    for (; x <= n; x += lowbit(x)) f[x] += y;
}
int ask(int x) {
    int ans = 0;
    for (; x; x -= lowbit(x)) ans += f[x];
    return ans;
}
int main() {
    //freopen("inversion.in", "r", stdin);
    //freopen("inversion.out", "w", stdout);
    scanf("%d", &n);
    rep(i, 1, n) scanf("%d", &nums[i]);
    scanf("%d", &q);
    urep(i, n, 1) {
        temp += ask(nums[i] - 1);
        add(nums[i], 1);
    }
    temp &= 1;
    rep(i, 1, q) {
        int x, y;
        scanf("%d%d", &x, &y);
        if (x != y)
            temp ^= 1;
        cout << temp << endl;
    }
    return 0;
}